Equilibrios de Oxido Reduccion

Las reacciones de óxido reducción son aquellas en las que sucede un intercambio de electrones de tal manera que hay un cambio en los estados de oxidación de las especies involucradas (posible cita). Su tratamiento puede darse enfocado en el cambio de potencial estándar como del potencial de electrones .

Enfoque – Potencial estándar de Reducción

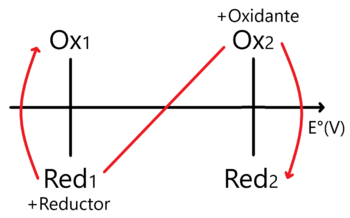
En este caso la regla de la N vista para sistemas Ácido - Base (posible link) se invierte en comparación a como la usamos en Ácidos y Bases.

Diagrama Unidimensional útil para sistemas de equilibrios Óxido-Reducción. Nótese dónde se ubican a los pares óxido-reductores según el potencial estándar de reducción (E°) de los mismos.

Nótese que en este caso ubicamos al Oxidante más fuerte en la parte superior derecha y al Reductor más fuerte en la inferior izquierda. En este sentido encontraremos el Proceso Espontáneo y cuya constante de equilibrio  se encuentra como:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \log_{10}(K_{eq})=\frac{\Delta E^{o} n_1 n_2}{0.06} }

Donde hemos de sustituir n₁ y n₂ como los electrones intercambiados por semirreacción involucrada.

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Ox1 + n1e^{-} <=> Red_1 -> E_1^{o}}}

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Ox2 + n2e^- <=> Red2 -> E2^{o}}}

Sólo en caso de que n₁ = n₂Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n_1 = n_2}  sustituimos a uno sólo de estos.

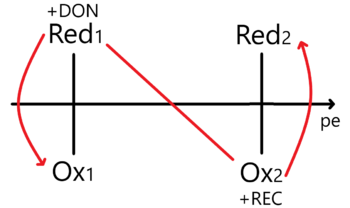
Enfoque – Potencial de electrones

Aquí es necesario plantear un equilibrio considerando una concentración de electrones. Para una reacción de la forma:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{a A + n e^- <=> b B + c C}}

Planteamos la constante de equilibrio y luego despejamos a la concentración de electrones Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle [e^{-}]} para aplicarle el cologaritmo correspondiente. Así obtenemos un potencial de electrón Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle pe^{-}} de tal manera que...

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle pe^{-} =\log_{10}{\frac{K_{eq}}{n}}+\log_{10}{\frac{[A]^{a}}{[B]^{b}[C]^{c}}}} Al hacer esto le estamos dando un tratamiento termodinámico. Ahora tenemos que representarlo en el DUZP.

Diagrama Unidimensional para sistemas de equilibrios óxido-reductores con enfoque en el potencial de electrón

La relación entre el potencial de electrones y el estándar de reducción viene dada por la ecuación:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \text{pe} \approx \frac{E}{0.06}}

Ecuación de Nerst

Aplica sólo para semirreacciones, de tal manera que:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{a Ox + n e^- <=> b Red }}

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E = E^{o} + \frac {0.06}{n} * \log_{10}{\frac {[Ox]^{a}}{[Red]^{b}}}}

Ejemplo 1: Titulación de una solución de estaño con permanganato

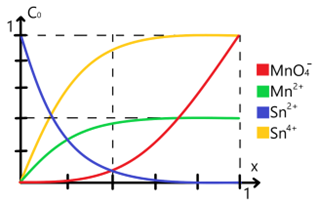
Para ejemplificarlo supongamos un sistema donde usamos permanganato Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{MnO4^-}} para valorar o titular una solución de iones de estaño Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Sn^{2+}}} para lo cual planteamos la siguiente reacción:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{2 MnO4^- + 5 Sn^2+ + 16 H^+ <=> 2 Mn^2+ + 5 Sn^4+ + 8 H2O }}

Esta reacción la planteamos conociendo los valores de potencial estándar de reducción para cada uno de los pares involucrados, la propia facultad de química de la UNAM tiene una tabla con los valores de potenciales estándar de reducción para muchas especies distintas. Según esta misma podemos apreciar que los valores implicados para estos pares son de +1.51 eV para el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{MnO4^- / Mn^{2+} }} y de +0.15 eV para el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Sn^{4+} / Sn^{2+} }} .La variación de las especies implicadas respecto al avance de la reacción es la siguiente:

Variación de especies en ejemplo REDOX

Nótese que aparecen amortiguadores cuando [Sn(2+)* = [Sn(4+)] y [MnO4(-)] = [Mn(2+)]. En estos casos podemos hacer uso del cálculo de potencial en el punto de equivalencia el cual se obtiene como:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \[ E = \frac{n_1 E_1^\circ + n_2 E_2^\circ}{n_1 + n_2} + \frac{0.06}{n_1 + n_2} \log\left( \frac{[\text{Ox}_1]^a [\text{Ox}_2]^b}{[\text{Red}_1]^a [\text{Red}_2]^b} \right) \] }

¡¡¡Recuerde que debe de sustituir los datos por semirreacción y no por la reacción global!!!

El análisis de potencial debe de llevarse a cabo considerando tres zonas. Por ejemplo, para la reacción:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \[ 6\,\text{Fe}^{2+}_{\text{analito}} + \text{Cr}_2\text{O}_7^{2-}_{\text{titulante}} \rightleftharpoons 2\,\text{Cr}^{3+} + 6\,\text{Fe}^{3+} \] }

·        Al inicio sólo hay Fe(2+) por lo que el  E(V) es indeterminado.

·        Antes del Punto de Equivalencia (APE) hay Fe(2+) y Cr(3+), el potencial entonces lo impone el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E_(Fe^(3+)/Fe^(2+)\ )=E_(Cr_2\ O_7^(2-)/Cr^(3+)\ )}

·        En la equivalencia la reacción no es cuantitativa, entonces usamos:

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E=(n_1\ E°_1+n_2 E°_2)/(n_1+n_2 )+0.06/(n_1+n_2 ) log⁡(([Ox_1 ]^a [Ox_2 ]^b)/([Red_1 ]^a [Red_2 ]^b ))}

·        Después del Punto de Equivalencia (DPE) el par que impone el potencial es

Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\textstyle E_(Cr_2\ O_7^(2-)/Cr^(3+)\ )}