Equilibrios de Oxido Reduccion
Las reacciones de óxido reducción son aquellas en las que sucede un intercambio de electrones de tal manera que hay un cambio en los estados de oxidación de las especies involucradas (posible cita). Su tratamiento puede darse enfocado en el cambio de potencial estándar como del potencial de electrones .
Enfoque – Potencial estándar de Reducción
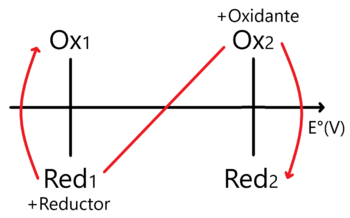
En este caso la regla de la N vista para sistemas Ácido - Base (posible link) se invierte en comparación a como la usamos en Ácidos y Bases.
Nótese que en este caso ubicamos al Oxidante más fuerte en la parte superior derecha y al Reductor más fuerte en la inferior izquierda. En este sentido encontraremos el Proceso Espontáneo y cuya constante de equilibrio se encuentra como:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \log_{10}(K_{eq})=\frac{\Delta E^{o} n_1 n_2}{0.06} }
Donde hemos de sustituir n1 y n2 como los electrones intercambiados por semirreacción involucrada.
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Ox1 + n1e^{-} <=> Red_1 -> E_1^{o}}}
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Ox2 + n2e^- <=> Red2 -> E2^{o}}}
Sólo en caso de que n1 = n2Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n_1 = n_2} sustituimos a uno sólo de estos.
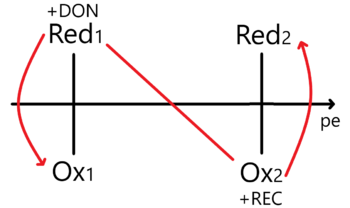
Enfoque – Potencial de electrones
Aquí es necesario plantear un equilibrio considerando una concentración de electrones. Para una reacción de la forma:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{a A + n e^- <=> b B + c C}}
Planteamos la constante de equilibrio y luego despejamos a la concentración de electrones Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle [e^{-}]} para aplicarle el cologaritmo correspondiente. Así obtenemos un potencial de electrón Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle pe^{-}} de tal manera que...
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle pe^{-} =\log_{10}{\frac{K_{eq}}{n}}+\log_{10}{\frac{[A]^{a}}{[B]^{b}[C]^{c}}}} Al hacer esto le estamos dando un tratamiento termodinámico. Ahora tenemos que representarlo en el DUZP.
La relación entre el potencial de electrones y el estándar de reducción viene dada por la ecuación:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \text{pe} \approx \frac{E}{0.06}}
Ecuación de Nerst
Aplica sólo para semirreacciones, de tal manera que:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{a Ox + n e^- <=> b Red }}
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E = E^{o} + \frac {0.06}{n} * \log_{10}{\frac {[Ox]^{a}}{[Red]^{b}}}}
Ejemplos
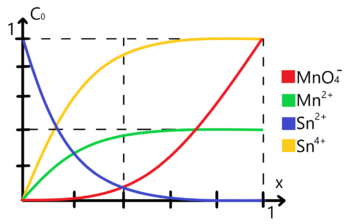
Variación de especies respecto al avance de reacción para la titulación de una solución de estaño con permanganato
Para ejemplificarlo supongamos un sistema donde usamos permanganato Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{MnO4^-}} para valorar o titular una solución de iones de estaño Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Sn^{2+}}} para lo cual consideramos los potenciales estándar de reducción Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{(E^{o}) }} para cada una de las especies involucradas; la propia facultad de química de la UNAM tiene una tabla con los valores de potenciales estándar de reducción para muchas especies distintas para lo cual consideraremos los valores de +1.51 eV para el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{MnO4^- / Mn^{2+} }} y de +0.15 eV para el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Sn^{4+} / Sn^{2+} }} .
Entonces las semirreacciones a considerar son:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{MnO4^- + 8 H^+ + 5 e^- <=> Mn^{2+} +4 H2O}} Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Sn^4+ + 2 e^- <=> Sn^{2+}}}
Entonces planteamos la siguiente reacción:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{2 MnO4^- + 5 Sn^2+ + 16 H^+ <=> 2 Mn^2+ + 5 Sn^4+ + 8 H2O }}
Si tienes dudas sobre cómo llegamos a esta conclusión considera revisar el tema balanceo ion electrón.
Para encontrar un gráfico de la variación de las especies implicadas respecto al avance de la reacción es necesario antes realizar la tabla y analizarla. A continuación te muestro dicha tabla simplificada (eliminamos a la concentración de protones porque decido ignorar el pH, así como la de agua porque asumimos que se encuentra en exceso):
Si deseas profundizar sobre cómo realizar este tipo de tablas considera revisar el tema tabla de variación de especies. Con la ayuda de esta tabla podemos realizar un gráfico que nos muestre cómo varía la concentración de cada una de las especies involucradas respecto al avance de la reacción tal, para ello tienes que considerar los siguientes puntos representándolos en el gráfico:
- Al inicio del sistema (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x = 0} ) sólo existe el analito Sn(2+) en el mismo en una concentración analítica Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_o} dada (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_o = 1} ). Si bien esta se encuentra en equilibrio con una cantidad dada de Sn(4+) esta está presente en cantidades Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_0} despreciables por ahora. Entonces colocaremos un punto azul en la coordenada (0,1).
- Aún en el inicio del sistema contemplamos que no hay ni una pizca de permanganato y mucho menos de ion manganeso, entonces colocamos puntos rojos y verdes en la coordenada (0,0).
- Conforme añadimos valorante (permanganato) el Sn(2+) se consume progresivamente y el permanganato totalmente (reacciona "casi" por completo) hasta alcanzar una paridad equimolar entre el titulante y el analito. Mientras este proceso ocurre decimos que estamos "Antes del Punto de Equivalencia" o A.P.E. y, cuando finalmente lo hemos alcanzado, estamos en el "Punto de Equivalencia" o P.E.
- En el P.E. (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x = \frac{2}{5}} ) asumiremos que las cantidades de analito y titulante son despreciables por ahora (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_2} ) aunque no necesariamente igual de insignificante a como lo estaba en Sn(4+) al principio del proceso, por eso manejamos distintas épsilon. Entonces colocaremos los puntos correspondientes en (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{2}{5}} ,0) para estas dos especies.
- Por otro lado, los productos de esta titulación deberían de haber alcanzado concentraciones equimolares respecto a lo añadido hasta ahora de titulante, de acuerdo a la tabla de variación de especies realizada anteriormente podemos ver que en este punto debería de haber Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{2}{5} C_o} de Mn(2+) así como de Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_o} de Sn(4+). Colocaremos los puntos correspondientes a una distancia de Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x = \frac{2}{5}} .
- "Después del Punto de Equivalencia" o D.P.E. no podremos generar más productos simplemente añadiendo más titulante, por lo que la concentración de estos permanece prácticamente constante así como lo que restaba de analito.
- Lo que sí varía es la concentración de titulante añadido, diremos que habremos de añadir suficiente hasta lograr igualar su concentración respecto a la que había originalmente de analito (Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_o = 1} ). Entonces le colocamos su respectivo punto en la coordenada (1,1).
- Finalmente unimos los puntos mediante líneas rectas, esta gráfica quedaría lista si tan sólo las cantidades Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon} fueran realmente insignificantes, algo curioso de la Química Analítica es que lo son hasta que de pronto dejan de serlo y este es uno de esos casos jaja. El gráfico que generaste con líneas rectas sólo aplica en reacciones completas y no en equilibrios químicos, entonces para corregirlo basta con "suavizar" tales líneas a curvas y comprender que esto sucede porque el sistema "siempre tiende a un equilibrio químico" de concentraciones; nota que en el P.E. si bien deberían de haberse consumido los reactivos, gracias a nuestro gráfico suavizado podemos apreciar que realmente aún están presentes aunque en cantidades "pequeñas".
Ahora que tenemos este gráfico es necesario generar uno que muestre la variación del potencial de reducción respecto al avance de reacción. Ya tenemos la mitad del trabajo hecho pues conocemos la tabla de variación de especies y con esta misma podemos obtener el potencial de reducción del sistema en cualquier momento dado simplemente aplicando la ecuación de Nerst.
Nótese que aparecen amortiguadores cuando Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{[Sn^{2+}] = [Sn^{4+}]}} y Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{[ MnO4^{-} ] = [ Mn^{2+} ]}} .
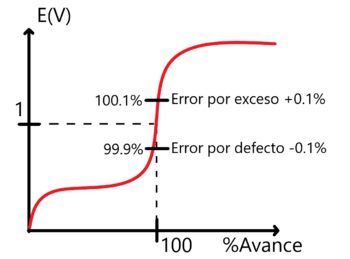
Análisis de la variación de potencial de reducción para una titulación de hierro con dicromato
El análisis de potencial debe de llevarse a cabo considerando tres zonas. Por ejemplo, para la reacción:
Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{6 Fe^2+ + Cr2O7^2- <=>2 Cr^3+ + 6 Fe^3+}} Con la ayuda de su tabla de variación de especies debemos de considerar las siguientes zonas:
- Al inicio sólo hay Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Fe^2+}} por lo que el E(V) es indeterminado.
- APE hay Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Fe^2+}} y Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ce{Cr^3+}} , el potencial entonces lo impone el par Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E_{Fe^{3+}/Fe^{2+}}} entonces podemos calcularlo a partir de la ecuación de Nerst.
- En el PE la reacción no es cuantitativa por lo que debemos de apoyarnos del cálculo de potencial en el punto de equivalencia y cual se obtiene como: Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E = \frac{n_{1}E_{1}^{o}+n_{2}E_{2}^{o}}{n_{1}+n_{2}}+\frac{0.06}{n_{1}+n_{2}} \log_{10}{\frac{[Ox_{1}]^{a}[Ox_{2}]^{b}}{[Red_{1}]^{a}[Red_{2}]^{b}}} } ¡¡¡Recuerda que debe de sustituir los datos por semirreacción y no según la reacción global!!!
- DPE el par que impone el potencial es el Error al representar (MathML con SVG o PNG como alternativa (recomendado para navegadores modernos y herramientas de accesibilidad): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\textstyle E_{Cr_{2}O_{7}^{2-}/Cr^{3+}}} así que nuevamente podemos hacer uso de la ecuación de Nerst para calcularlo.
Así, el gráfico que obtenemos es el siguiente: